Was in aller Welt hat Évariste Galois damit zu tun?
Bevor wir in das kryptografische Kaninchenloch eintauchen, lassen Sie uns klären, was Galois-Felder eigentlich sind. Benannt nach dem jungen französischen Mathematiker Évariste Galois (der, Fun Fact, mit 20 Jahren in einem Duell starb - ein wahrhaft dramatischer Abgang), sind diese Felder endliche Mengen von Elementen mit besonderen algebraischen Eigenschaften.
Einfacher ausgedrückt: Stellen Sie sich einen Spielplatz vor, auf dem Zahlen nach sehr spezifischen Regeln spielen. Diese Regeln sorgen dafür, dass Sie, egal wie Sie diese Zahlen addieren, subtrahieren, multiplizieren oder dividieren (außer durch null, denn selbst in der Mathematik können wir nicht durch null teilen), immer wieder bei einer Zahl auf demselben Spielplatz landen.
Die Verbindung zur Kryptografie: Warum Galois-Felder wichtig sind
Jetzt denken Sie vielleicht: "Coole Geschichte, aber was hat das damit zu tun, meine Katzen-Memes vor neugierigen Blicken zu schützen?" Gute Frage! Galois-Felder sind das Rückgrat mehrerer weniger bekannter, aber zunehmend wichtigerer kryptografischer Systeme. Hier ist der Grund, warum sie für Aufsehen sorgen:
- Effizienz: Operationen in Galois-Feldern können unglaublich schnell und effizient sein, was für die Echtzeitverschlüsselung entscheidend ist.
- Widerstandsfähigkeit: Sie bieten starken Schutz gegen bestimmte Arten von kryptografischen Angriffen.
- Flexibilität: Galois-Felder unterschiedlicher Größen können verwendet werden, um verschiedene Sicherheitsstufen zu schaffen, was sie anpassungsfähig an unterschiedliche Bedürfnisse macht.
Galois-Felder in Aktion: Kryptografische Systeme in der Praxis
Werfen wir einen Blick auf einige kryptografische Systeme, die Galois-Felder nutzen:
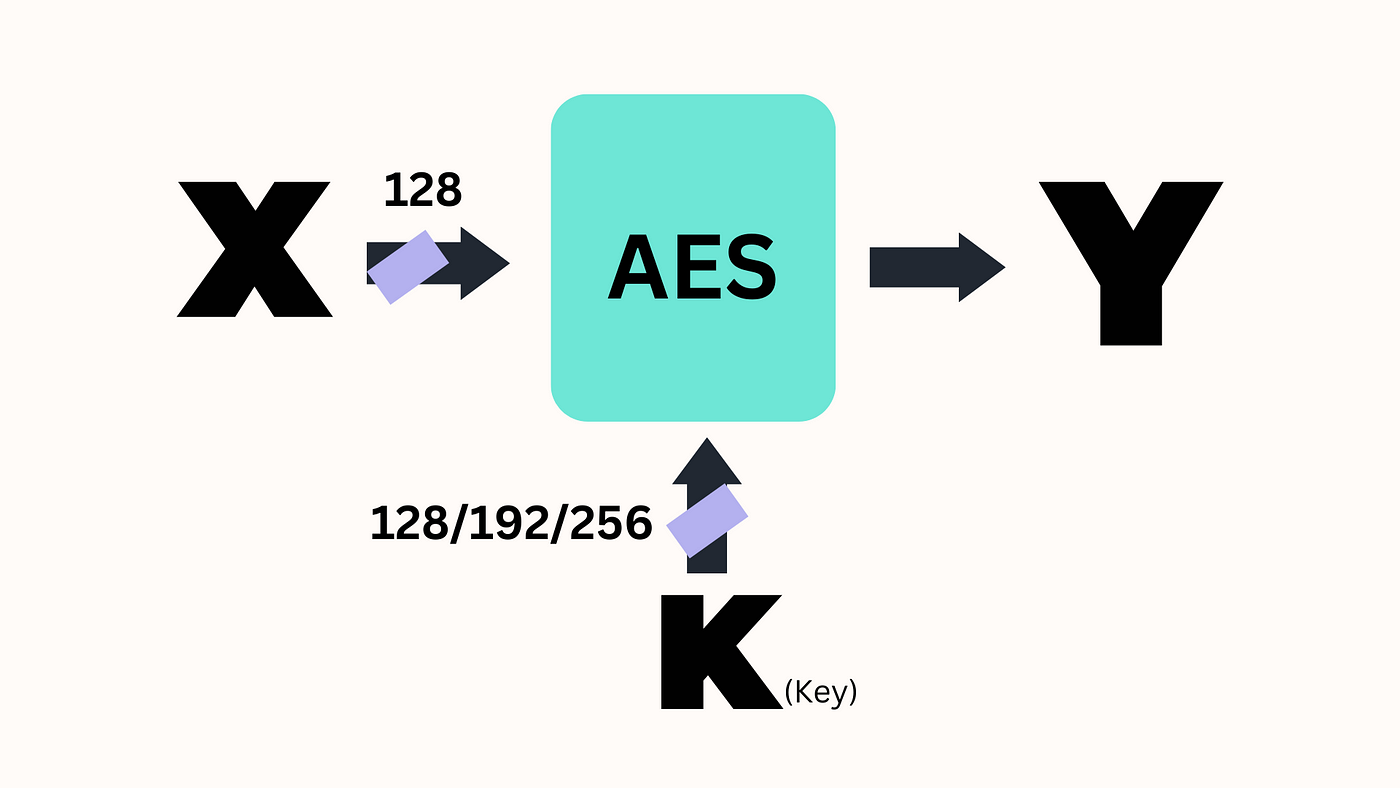
1. Advanced Encryption Standard (AES)
Ja, genau der AES. Obwohl nicht gerade "next-gen", verwendet AES Operationen im Galois-Feld GF(2^8) für seinen MixColumns-Schritt. Dies hilft, die Verwirrung und Verteilung zu schaffen, die für sichere Verschlüsselung notwendig sind.
2. Reed-Solomon-Fehlerkorrektur
Obwohl hauptsächlich zur Fehlerkorrektur bei der Datenübertragung und -speicherung verwendet, haben Reed-Solomon-Codes, die auf Galois-Feld-Arithmetik basieren, auch Anwendungen in der Kryptografie, insbesondere in Geheimteilungsverfahren.
3. Elliptische-Kurven-Kryptografie (ECC)
ECC arbeitet über endlichen Feldern, oft Galois-Feldern. Dies ermöglicht kleinere Schlüssellängen im Vergleich zu RSA bei gleichbleibendem Sicherheitsniveau.
Die nächste Grenze: Post-Quanten-Kryptografie
Hier wird es wirklich interessant. Da Quantencomputer am Horizont auftauchen und drohen, viele unserer aktuellen Verschlüsselungsmethoden zu brechen, wenden sich Kryptografen Galois-Feldern zu, um quantenresistente Algorithmen zu entwickeln.
Code-basierte Kryptografie
Ein vielversprechender Bereich ist die code-basierte Kryptografie, die stark auf Operationen in Galois-Feldern angewiesen ist. Das McEliece-Kryptosystem verwendet beispielsweise fehlerkorrigierende Codes über endlichen Feldern, um ein Public-Key-Verschlüsselungssystem zu schaffen, das als quantenresistent gilt.
Hier ist ein vereinfachtes Beispiel, wie ein Galois-Feld in der code-basierten Kryptografie verwendet werden könnte:
import galois
# Erstellen Sie ein Galois-Feld der Größe 2^8
GF = galois.GF(2**8)
# Generieren Sie eine zufällige Nachricht
message = GF.Random(10)
# Generieren Sie einen zufälligen Fehlervektor
error = GF.Random(10)
# Simulieren Sie das Kodieren und Hinzufügen von Fehlern
encoded_message = message + error
# In Wirklichkeit würde das Dekodieren komplexe Algorithmen
# unter Verwendung der Eigenschaften des Galois-Feldes erfordern
decoded_message = encoded_message - error
print(f"Originalnachricht: {message}")
print(f"Dekodierte Nachricht: {decoded_message}")
print(f"Sind sie gleich? {all(message == decoded_message)}")
Dies ist natürlich ein sehr vereinfachtes Beispiel. Echte code-basierte Kryptosysteme beinhalten viel komplexere Operationen und größere Feldgrößen.
Herausforderungen und Überlegungen
Bevor Sie losziehen und all Ihren Kryptocode mit Galois-Feldern umschreiben, sollten wir einige Herausforderungen betrachten:
- Komplexität: Die Arbeit mit Galois-Feldern erfordert ein solides Verständnis der abstrakten Algebra. Es ist nichts für schwache Nerven (oder Mathematik).
- Implementierung: Die effiziente Implementierung von Galois-Feld-Arithmetik kann knifflig sein, insbesondere auf Hardware, die nicht für diese Operationen optimiert ist.
- Standardisierung: Viele auf Galois-Feldern basierende Kryptosysteme befinden sich noch in der Forschungsphase und sind noch nicht weit verbreitet standardisiert.
Also, was ist das große Ding?
Galois-Felder sind mehr als nur eine mathematische Kuriosität. Sie bilden die Grundlage für eine neue Generation von kryptografischen Systemen, die schneller, effizienter und potenziell quantenresistent sein könnten. Da wir in eine Ära eintreten, in der Datensicherheit wichtiger denn je ist, werden diese mathematischen Strukturen wahrscheinlich eine zunehmend wichtige Rolle dabei spielen, unser digitales Leben sicher zu halten.
Ob Sie ein Kryptografie-Enthusiast, ein Sicherheitsexperte oder einfach jemand sind, der auf Partys klug klingen möchte, das Verständnis der Rolle von Galois-Feldern in der modernen Kryptografie ist definitiv Ihre Zeit wert. Wer weiß? Der nächste Durchbruch in der Datensicherheit könnte genau aus diesen endlichen Feldern mit unendlichen Möglichkeiten kommen.
"Die Kunst der Mathematik besteht darin, den speziellen Fall zu finden, der alle Keime der Allgemeinheit enthält." - David Hilbert
Und im Fall der modernen Kryptografie könnte dieser spezielle Fall genau die Galois-Felder sein. Also, wenn Sie das nächste Mal jemand nach der Zukunft der Verschlüsselung fragt, können Sie selbstbewusst sagen: "Es dreht sich alles um Galois, 'bout that Galois, kein Problem."
Weiterführende Lektüre
Wenn Sie neugierig geworden sind und tiefer in die Welt der Galois-Felder und ihre Anwendungen in der Kryptografie eintauchen möchten, hier sind einige Ressourcen, um Ihnen den Einstieg zu erleichtern:
- Galois: Eine Python 3 Bibliothek für Galois-Feld-Arithmetik
- NIST-Bericht über Post-Quanten-Kryptografie
- Handbuch der elliptischen und hyperelliptischen Kurvenkryptografie
Denken Sie daran, in der Welt der Kryptografie ist das, was heute hochmodern ist, morgen schon veraltet. Bleiben Sie neugierig, lernen Sie weiter, und wer weiß? Vielleicht sind Sie derjenige, der das nächste große Ding in der Kryptografie entdeckt. Möge der Galois mit Ihnen sein!