Präzision ist in der Welt des maschinellen Lernens von großer Bedeutung. Sie entscheidet darüber, ob deine KI eine Katze erkennt oder denkt, sie sieht einen Toaster. Aber hier kommt der Clou – manchmal ist mehr Präzision nicht immer besser. Hier kommt das stochastische Runden ins Spiel.
Stochastisches Runden 101
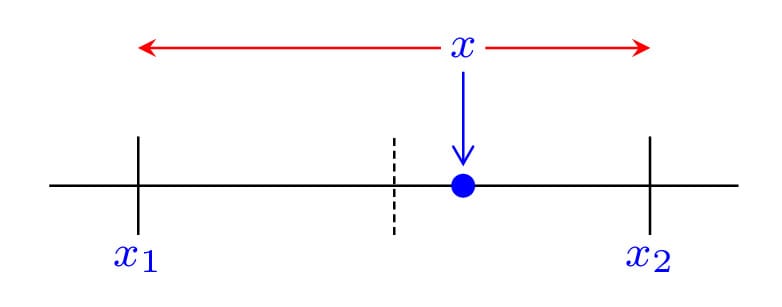
Was genau ist diese magische Technik? Einfach ausgedrückt, ist stochastisches Runden eine Methode, bei der Zahlen mit einer gewissen Zufälligkeit gerundet werden. Anstatt immer auf den nächsten Wert zu runden, wird manchmal basierend auf Wahrscheinlichkeiten auf- oder abgerundet.
Hier ein kurzes Beispiel:
import random
def stochastic_round(x):
floor = int(x)
return floor + (random.random() < (x - floor))
# Beispielverwendung
print(stochastic_round(3.7)) # Könnte 3 oder 4 sein
print(stochastic_round(3.7)) # Könnte 3 oder 4 sein
print(stochastic_round(3.7)) # Könnte 3 oder 4 sein
Führe dies ein paar Mal aus, und du wirst sehen, dass 3.7 nicht immer zu 4 gerundet wird. Manchmal ist es 3, manchmal 4. Es ist wie Schrödingers Runden – sowohl auf- als auch abgerundet, bis du es beobachtest!
Warum ist das wichtig?
Jetzt denkst du vielleicht: "Großartig, wir haben Zufälligkeit eingeführt. Wie hilft das?" Nun, mein skeptischer Freund, lass mich die Vorteile aufzählen:
- Reduzierte Verzerrung: Traditionelles Runden kann systematische Verzerrungen einführen, besonders bei vielen kleinen Werten. Stochastisches Runden hilft, dies zu mildern.
- Bessere Gradientenabschätzungen: Im Deep Learning kann stochastisches Runden zu genaueren Gradientenabschätzungen während der Rückpropagation führen.
- Verbesserte Konvergenz: Einige Studien haben gezeigt, dass stochastisches Runden helfen kann, dass neuronale Netze schneller und zu besseren Optima konvergieren.
- Hardware-Effizienz: Es ermöglicht die Nutzung von Hardware mit geringerer Präzision, während hochpräzise Ergebnisse beibehalten werden.
Auswirkungen in der realen Welt
Noch nicht überzeugt? Schauen wir uns einige konkrete Beispiele an, bei denen stochastisches Runden Wellen schlägt:
1. Training mit geringerer Präzision
Forscher bei Facebook AI Research (jetzt Meta AI) haben herausgefunden, dass sie mit stochastischem Runden große Sprachmodelle mit 8-Bit-Präzision trainieren konnten, ohne an Genauigkeit zu verlieren. Das ist enorm für die Reduzierung des Speicherbedarfs und der Rechenanforderungen.
2. Verbesserte Quantisierung
Googles TPU (Tensor Processing Unit) verwendet stochastisches Runden in seinem bfloat16-Format, was schnelleres Training und Inferenz ermöglicht, ohne die Modellqualität zu opfern.
3. Wissenschaftliches Rechnen
Außerhalb des maschinellen Lernens wird stochastisches Runden in Klimamodellen und Strömungsdynamik-Simulationen eingesetzt, um die Genauigkeit bei der Verwendung von Arithmetik mit geringerer Präzision zu erhalten.
Die Schattenseite des stochastischen Rundens
Bevor du jetzt losrennst, um stochastisches Runden überall zu implementieren, lass uns über einige potenzielle Fallstricke sprechen:
- Reproduzierbarkeit: Die Zufälligkeit im stochastischen Runden kann die exakte Reproduzierbarkeit von Ergebnissen erschweren.
- Overhead: Das Generieren von Zufallszahlen für das Runden kann zu einem Rechenaufwand führen.
- Nicht immer vorteilhaft: In einigen Fällen, insbesondere bei sehr tiefen Netzwerken, könnten die Vorteile weniger ausgeprägt sein.
"Mit großer Macht kommt große Verantwortung" - Onkel Ben (und jeder Datenwissenschaftler, der stochastisches Runden verwendet)
Implementierung von stochastischem Runden
Neugierig, es auszuprobieren? Hier ist eine umfassendere Python-Implementierung, mit der du experimentieren kannst:
import numpy as np
def stochastic_round(x, precision=1):
scale = 10 ** precision
scaled = x * scale
floor = np.floor(scaled)
prob = scaled - floor
rounded = floor + (np.random.random(x.shape) < prob)
return rounded / scale
# Beispielverwendung
x = np.array([1.34, 2.67, 3.45, 4.82])
print("Original:", x)
print("Stochastisch gerundet:", stochastic_round(x))
print("Numpy round:", np.round(x))
Führe dies ein paar Mal aus und vergleiche die Ergebnisse. Du wirst sehen, dass stochastisches Runden manchmal unterschiedliche Ergebnisse liefert, während numpy's round immer konsistent ist.
Die Zukunft der Präzision
Da maschinelle Lernmodelle immer größer und komplexer werden, werden Techniken wie stochastisches Runden zunehmend wichtig. Wir sehen bereits, dass Hardwarehersteller wie NVIDIA Unterstützung für stochastisches Runden in ihren neuesten GPUs integrieren.
Was kommt als Nächstes? Einige Bereiche, die man im Auge behalten sollte:
- Hybrid-Präzisionstraining: Kombination verschiedener Präzisionen und Rundungsmethoden für verschiedene Schichten oder Operationen.
- Adaptives stochastisches Runden: Dynamische Anpassung des Rundungsverhaltens basierend auf dem aktuellen Trainingszustand.
- Hardware-Beschleunigung: Mehr dedizierte Hardwareunterstützung für effiziente stochastische Rundungsoperationen.
Zusammenfassung
Stochastisches Runden mag im großen Schema des maschinellen Lernens wie ein kleines Detail erscheinen, aber es sind diese Arten von Innovationen, die das Feld voranbringen. Es ermöglicht uns, größere Modelle effizienter zu trainieren, Simulationen mit größerer Genauigkeit durchzuführen und die Grenzen des Möglichen mit begrenzten Hardware-Ressourcen zu erweitern.
Also, das nächste Mal, wenn dich jemand nach dem neuesten Stand der Technik im ML fragt, sprich nicht nur über Transformer oder Reinforcement Learning. Erwähne stochastisches Runden und beobachte, wie ihre Augen aufleuchten... ich meine, vor Aufregung strahlen!
Denkanstöße
Bevor du gehst, hier ein paar Fragen zum Nachdenken:
- Wie könnte stochastisches Runden die Interpretierbarkeit von Modellen beeinflussen?
- Könnten stochastische Rundungstechniken verwendet werden, um die Privatsphäre in föderierten Lernumgebungen zu verbessern?
- Welche anderen Bereiche der Informatik oder des Ingenieurwesens könnten vom stochastischen Runden profitieren?
Denk daran, in der Welt des maschinellen Lernens kann manchmal ein wenig Zufälligkeit zu viel Präzision führen. Gehe nun hinaus und runde stochastisch!